Understanding Transformers Part 2 : Building Blocks

In this post, we will continue from where we left off in the last post. We will march on towards our ultimate goal of implementing a Transformer from scratch. The full implementation of the Transformer can be found here
We will use the PyTorch Framework to create our implementation of the Transformer. Also, as mentioned previously, our implementation is based on the Attention is All you Need Paper by Vaswani et. al. found here.
A Note before we start
Note: It is important to note that the original paper can get pretty technical if you are new to Transformers or Natural Language Processing or are reading this paper for the first time.
As a result, instead of first trying to go through each and every concept of the Transformer, we will understand and implement each element of the Transformer as and when it comes along in the overall architecture of the Transformer.
This will give our learning journey a sequential experience without having to take frequent and recurrent detours to the basics. If you don’t understanding something or anything in the diagram, it is completely fine! We will understand and implement these blocks as we move forward!
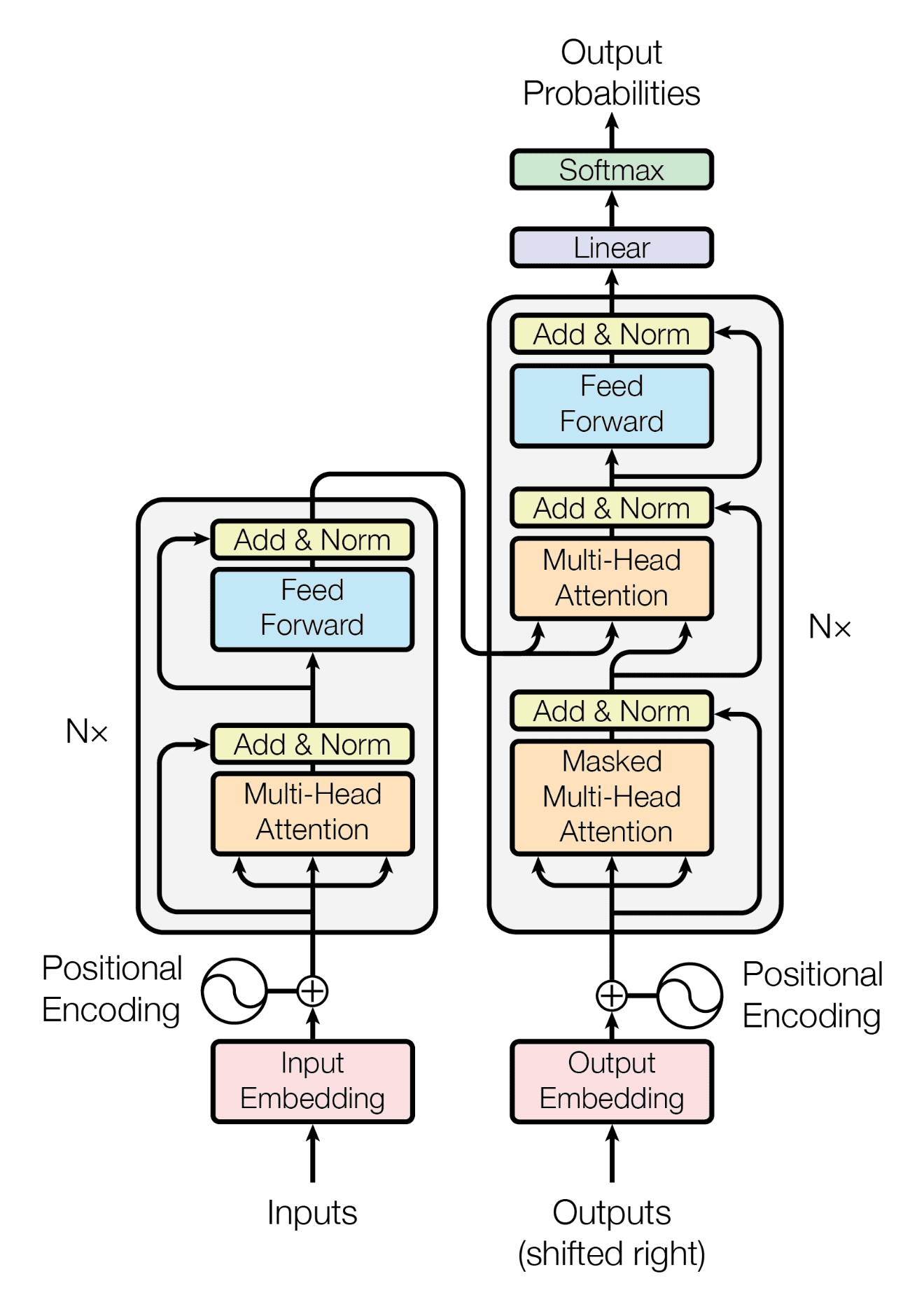
Introduction
In this post, we will focus on implementing all the building blocks of the Transformer Architecture. Since the Encoder and the Decoder (explained later), are the core parts of the Transformer, the parts that we will focus on in this post also serve as the building blocks of the Encoder and the Decoder. Let’s begin!
We saw in the previous post that we must process our input sentence by converting words into one-hot vectors that we later process to neural networks so that we can make the network learn from the inputs and establish an input-output mapping through the backpropagation algorithm.
However, as we can see, only having a one hot vector in the dimension of the vocabulary limits our ability to be expressive when it comes to learning.
We want to use not just one position of the vector, as is the case for one-hot vectors, but we want to use all the positions in the vector. Moreover, we don’t want to use just a single number for representing a whole word. Instead, we would like to use all real-valued numbers for our purposes.
As is evident, we would like to use the whole vector and have real-valued values across each and every position.
Enter: The Embedding Matrix
For this very exact purpose, we have the Embedding Matrix. An Embedding Matrix does as its name suggests. It takes a one-hot vector in a certain dimension ‘N’ and then projects that vector into another dimension ‘M’ having real-valued numbers across all of the positions of the vector.
This is enabled by the Embedding Matrix. In technical terms, an Embedding Matrix is a Linear Transformation that takes an ‘N-dimensional’ vector and projects it into an ‘M-dimensional’ vector.
Therefore, for the case mentioned above, the Embedding Matrix is an N x M Matrix for our purposes. For the purposes of the Transformer, we tokenize each sentence (a collection of words) and then apply the Input Embeddings to the said tokenized input.
We can take example values for our purposes. Let N = 3 and M = 5, then we have the following vectors and matrices.
For the input vector, which looks like the first word in language that has a vocabulary of 3 words, we have:
\[\begin{bmatrix} 1 \cr 0 \cr 0 \end{bmatrix}\]The Embedding Matrix would be initialized as a random 3 x 5 Matrix. Note that Embedding Matrix would also be a part of the learning algorithm and therefore would be adjusted by the gradients for the errors in the outputs obtained from the backpropagation algorithm.
The Embedding Matrix could look as follows:
\[\begin{bmatrix} 1 & 2 & 3 & 4.5 & 5.25\\ 6.6 & 7.1 & 8.2 & 9 & 10\\ 11.8 & 12 & 13 & 14.3 & 15 \end{bmatrix}\]If we multiply the input vector with the embedding matrix, we get the output vector in 1 x 5 dimensions, or the embedded vector, as follows:
Mathematically, this is all that we need to understand about the Embedding Matrix!
Building Code Blocks
We can see how this is done in code now. We create a file called transformer.py, but you are free to give it any name you wish.
Before we start, we need to do the following imports:
import torch
import torch.nn as nn
import numpy as np
After this is done, we can now set up some parameters and implement the word and sentence tokenization architecture. We will first create some parameters as shown below. Some of these won’t be obvious right now and they will be explained in detail further in this post.
# we have a total vocabulary of 747 words
vocab_size = 747
# we choose 12 words per sentence
context_length = 12
# we chose 9 sentences at a time
batch_size = 9
# D_MODEL here is basically `H` number of attention heads, each producing outputs in the `D_V` dimension, concatenated
D_MODEL = 512
# we define the number of attention heads
NUM_HEADS = 8
# we also define the `D_K` and `D_V` parameters for the encoder and decoder
D_K = int(D_MODEL / NUM_HEADS)
D_V = int(D_MODEL / NUM_HEADS)
# set up the training output parameters for the decoder
# vocabulary size for the outputs
output_vocab_size = 879
print('Transformer Model Parameters Loaded...')
print(f'dk = {D_K}; dv = {D_V}; dmodel = {D_MODEL}')
The vocab_size is a variable that we have created regarding the vocabulary size of our input language. The context_length is a variable that describes how many words from the input sequence will we consider at once when producing an output using the Transformer. The batch_size variable decides how many sentences will we process at once.
Do not worry about the D_MODEL, NUM_HEADS, D_K, D_V variables right now! They are all variables that we will explain later in this post.
In the end, we just print the values of the variables as a quick logging exercise.
Preparing the Tokenizations
Now we begin the process of tokenizing our inputs and applying the embeddings to the inputs so that we may feed these inputs to the Transformer. We start by one-hot encoding the words.
def create_one_hot_vector(ix, vocab_size):
one_hot_vector = torch.zeros((1, vocab_size))
# the vector has the value of `1` at the indicated index and is `0` everywhere else
one_hot_vector[0][ix] = 1
return one_hot_vector
As is evident, this piece of code takes an ix value (an index value) and then creates a vector of vocab_size dimension, of all zeros and sets the ix position to 1. Remember that we have zero-indexing so that the first index is 1. We then return the vector.
Now, we will build the vocabulary tokens for each word in our vocabulary. Right now, we will create a function for taking random words and preparing their tokens.
def create_vocab_tokens(vocab_size):
word_tokens = []
for num in range(vocab_size):
# one hot vector for each word
one_hot_vector = create_one_hot_vector(num, vocab_size=vocab_size)
word_tokens.append(one_hot_vector)
word_tokens_tensor = torch.stack(word_tokens).squeeze()
return word_tokens_tensor
This piece of code runs a for loop vocab_size times and in each iteration, it creates a one-hot vector for each word in the vocabulary. We maintain a list of word_tokens and add each one-hot vector to that token.
We ultimately create a PyTorch tensor of this list so that we may feed this tensor to our Embedding Matrix and we apply the .squeeze() method to remove the extra dimension that is added when we apply the .stack() method to the tokens.
Now, we create the input and output tokens for the purposes of training.
# prepare tokens for the vocabulary for input data
input_vocab_word_tokens = create_vocab_tokens(vocab_size=vocab_size)
# prepare tokens for the vocabulary for output data
output_vocab_word_tokens = create_vocab_tokens(vocab_size=output_vocab_size)
Finally, we will implement the sentence tokenization code that will help us in creating the tokens of words in one go.
def create_sentence_token(ctx_length, vocabulary_size, data_type='input'):
word_tokens = []
# get random word choices `context_length` times from the vocabulary. `context_length`
# here denotes the number of words per sentence
word_choices = torch.randint(0, vocabulary_size, (1, ctx_length), dtype=torch.long)
for i in range(ctx_length):
# choose the token for each of the generated index
if data_type == 'input':
token = input_vocab_word_tokens[word_choices[0][i]]
else:
token = output_vocab_word_tokens[word_choices[0][i]]
word_tokens.append(token)
# stack the words to form a sentence
sentence_token = torch.stack(word_tokens, dim=0).squeeze()
return sentence_token
In the above code, we create random sentences, in the sense that we generate random integers in the range of 0 to vocabulary_size of dimension 1 x ctx_length. ctx_length here stands for ‘context length’ .
Next, we run a for loop as many times as ctx_length and on each iteration, we create a token by choosing the word from the input tokens or output tokens depending on whether the sentences are being generated for the input or for the output during training, as indicated by the data_type variable.
In the end, we merge all the words together using the torch.stack method on the word tensors and clean up the final stray dimension using the .squeeze() method.
Finally, we create one function to combine and execute all the functions defined above at once:
def create_sentence_batches(batch_size_, ctx_length, vocabulary_size, data_type='input'):
sentence_batches = []
if data_type == 'input':
for _ in range(batch_size_):
# create tokens for each sentence
sentence_tokens = create_sentence_token(ctx_length=ctx_length, vocabulary_size=vocabulary_size, data_type=data_type)
sentence_batches.append(sentence_tokens)
elif data_type == 'output':
for _ in range(batch_size_):
# create tokens for each sentence
sentence_tokens = create_sentence_token(ctx_length=ctx_length, vocabulary_size=vocabulary_size, data_type=data_type)
sentence_batches.append(sentence_tokens)
# stack sentences to form a batch
sentence_batch_tokens = torch.stack(sentence_batches, dim=0)
return sentence_batch_tokens
As can be seen, this function creates sentence tokens using the functions we described above and gives us batches of sentence tokens that are multi-dimensional and real-valued vectors representing words in a given language of our choosing and we are ready to use these words now for training our Transformer!
Embedding the Tokenizations
Now that we have our tokens in the form of one-hot vectors for each sentence in our dataset, we will now create the training data sentence batches apply the embedding layer to them in our code using PyTorch.
# create training inputs
training_data_inputs = create_sentence_batches(batch_size_=batch_size,
ctx_length=context_length,
vocabulary_size=vocab_size,
data_type='input')
# create training outputs
training_data_outputs = create_sentence_batches(batch_size_=batch_size,
ctx_length=context_length,
vocabulary_size=output_vocab_size,
data_type='output')
print(f'Training Data Inputs Shape: {training_data_inputs.shape}')
print(f'Training Data Outputs Shape: {training_data_outputs.shape}')
# the embedding layer takes an input in `vocab_size` dim and projects it to `D_MODEL` dim
embedding_layer = nn.Linear(vocab_size, D_MODEL)
embeddings = embedding_layer(training_data_inputs)
Now, since our progression for understanding and implementing the Transformers is based on the chronology in which the elements appear in the model itself, we will revisit the Transformer Architecture diagram once more to understand the next part we need to understand.

Positional Encoding
As can be seen in the diagram, the next bit after the Inputs and the Embeddings is the Positional Encoding layer. The way to understand this layer is very simple.
We have tokens for the words and even for the sentences, but when it comes to language, we want our Neural Network to understand the position of each word in the sentence. For example, we want the sentence ‘The sun shines’ to make more sense to our Transformer as compared to the sentence ‘shines The sun’ .
Now, if we create one-hot vectors of the above sentence, that is, of, _‘The sun shines’ _, then as seen in Part 1 of the blog this series, we might have a representation such as:
\[The \begin{bmatrix} 1 \cr 0 \cr 0 \end{bmatrix}\] \[Sun \begin{bmatrix} 0 \cr 1 \cr 0 \end{bmatrix}\] \[Shines \begin{bmatrix} 0 \cr 0 \cr 1 \end{bmatrix}\]Now, if we take the sentence ‘shines The sun’, the sequence of the one-hot vector would look as follows:
\[shines \begin{bmatrix} 0 \cr 0 \cr 1 \end{bmatrix}\] \[The \begin{bmatrix} 1 \cr 0 \cr 0 \end{bmatrix}\] \[sun \begin{bmatrix} 0 \cr 1 \cr 0 \end{bmatrix}\]For this reason, we give our model a sense of the position of every word in our sentence relative to other words in the sentence. The specific formulas are as shown below:
As you can see, a token in the sentence having an even-numbered dimension sits on a sine wave and a token in the sentence on an odd-numbered dimension sits on a cosine wave. The sinusoidal nature of the waves lets us
Conclusion
Now that we have understood and implemented the positional encoding layer, we will stop here. That’s it for now.
If this is the first time that you are reading up on the topic of Transformers, it may take you some time to understand and make sense of this code, go through it again and slowly and try to focus on the fundamentals and you would understand it in no time!
Now that we have our input data and output data tokenized and embedded even positionally, in the next post, we can begin building the Encoder and the Decoder, after which our Transformer would be ready!